[adsp] 주성분분석(PCA. Principal Component Analysis)

1. 주성분분석(PCA. Principal Component Analysis)
여러 독립변수들을 주성분이라는 서로 상관성이 낮은 변수들의 선형결합으로 만들어 변수들을 요약, 축소하는 기법이다.
- 공분산행렬이나 상관계수행렬을 통해 모든 변수들을 잘 설명해주는 주성분을 찾는다.
- 독립변수들과 주성분과의 거리를 나타내는 정보손실량을 최소화하고 분산을 최대화한다.
- 제1주성분이 전체 변동을 최대로 설명할 수 있어야 하고 제2주성분은 제1주성분과 상관성이 낮아 제1주성분이 설명하지 못하는 나머지 변동을 가장 잘 설명할 수 있어야 한다.
* 공분산행렬과 상관계수행렬의 차이
| 공분산행렬 | 상관계수행렬 | |
| 변수의 측정단위를 그대로 반영한다. | 변수의 측정단위를 표준화한다. | |
| 특징 | 변수들의 측정단위에 민감하다. | |
| 사용 사례 | 모든 변수들이 같은 수준으로 점수화된 설문조사에서 사용한다. | 변수들의 scale이 많이 다를 경우 사용한다. |
2. 주성분분석의 목적
여러 변수들간에 내재하는 상관관계를 소수의 주성분으로 나타냄으로서 차원을 축소하고 데이터 관리를 쉽게 한다.
회귀분석이나 의사결정나무 같은 모형을 개발할 때 설명 변수간의 상관관계가 높아 다중공선성이 존재하게 된다. 이때 주성분분석으로 상관성이 적은 주성분으로 변수들을 축소하여 모형을 개발할 수 있다.
3. 주성분분석과 요인분석의 차이
| 주성분분석(PCA) | 요인분석(Factor Analysis) | |
| 공통점 | 데이터를 축소하여 몇 개의 새로운 변수들을 생성한다. | |
| 생성된 변수의 개수 | 제1주성분, 제2주성분, 제3주성분을 활용한다. (보통 4개 이상은 넘지 않음) | 제약 없음 |
| 생성된 변수명 | 제n주성분(n=1,2,3 ..) | 분석자가 요인을 명명한다. |
| 생성된 변수간의 관계 | 제1주성분이 가장 중요하고 순차적으로 중요하게 취급된다. | 모든 변수들은 대등한 관계를 가진다. 만약 분류/예측의 다음 단계로 활용된다면 그때 변수 간의 중요성이 달라진다. |
| 분석기법의 의미 | 목표변수를 고려하여 목표변수를 잘 분류/예측하기 위한 주성분들을 찾아낸다. | 목표변수 고려 없이 비슷한 성격들로 묶어서 새로운 변수를 생성한다. |
4. 주성분분석 해석
- 표준편차(Standard Deviation): 자료의 산포도를 나타내는 수치. 표준편차가 작을수록 평균과 변량의 거리는 가깝다.
- 분산비율(Proportion of Variance): 전체 분산에서 각 분산이 차지하는 비율
- 누적비율(Cumulative Proportion): 분산의 누적 비율
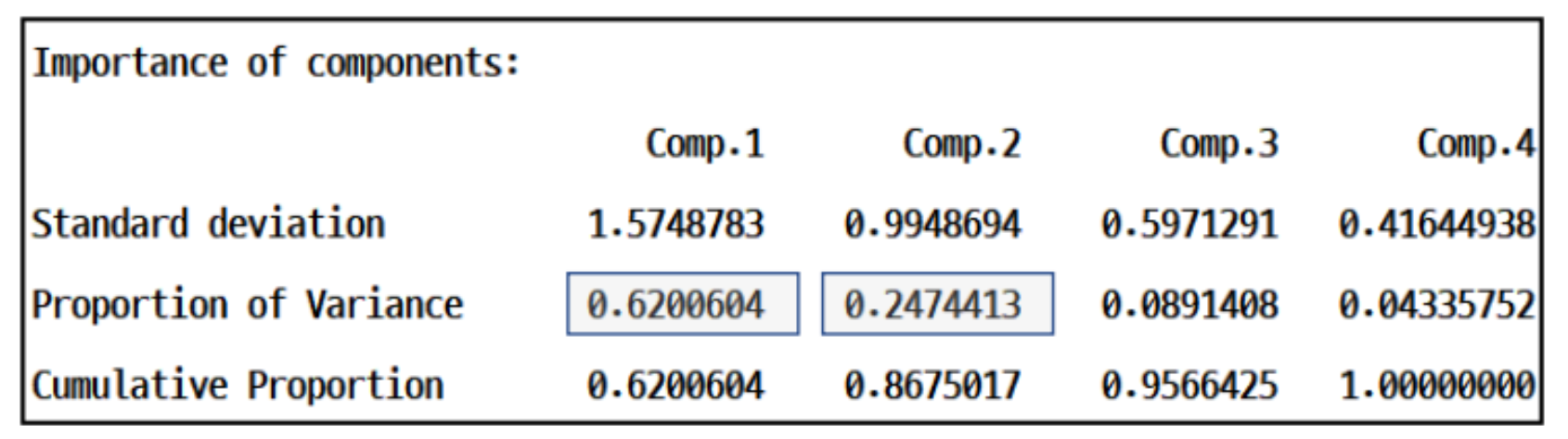
해석)
- 제1주성분으로 전체 분산의 62%를 설명할 수 있다. (제1주성분의 분산비율)
- 두 개의 주성분으로 자료를 축약할 때 전체 분산의 86.7%를 설명할 수 있다. (제2주성분의 누적비율)
- 정보손실율을 5% 이하로 변수를 축약한다면 세 개의 주성분을 사용하는 것이 바람직하다. (100-95.6=4.4<5)
- 누적비율이 85% 이상이면 주성분 수로 결정할 수 있으므로 주성분은 2개가 적합하다.
5. 주성분분석 시 고려사항들
1) 공분산행렬과 상관계수행렬 중 무엇을 선택할까?
2) 주성분 개수를 몇 개로 할 것인가?
3) 주성분에 영향을 주는 변수로 어떤 독립변수를 선택할 것인가?
참고
https://airsbigdata.tistory.com/118