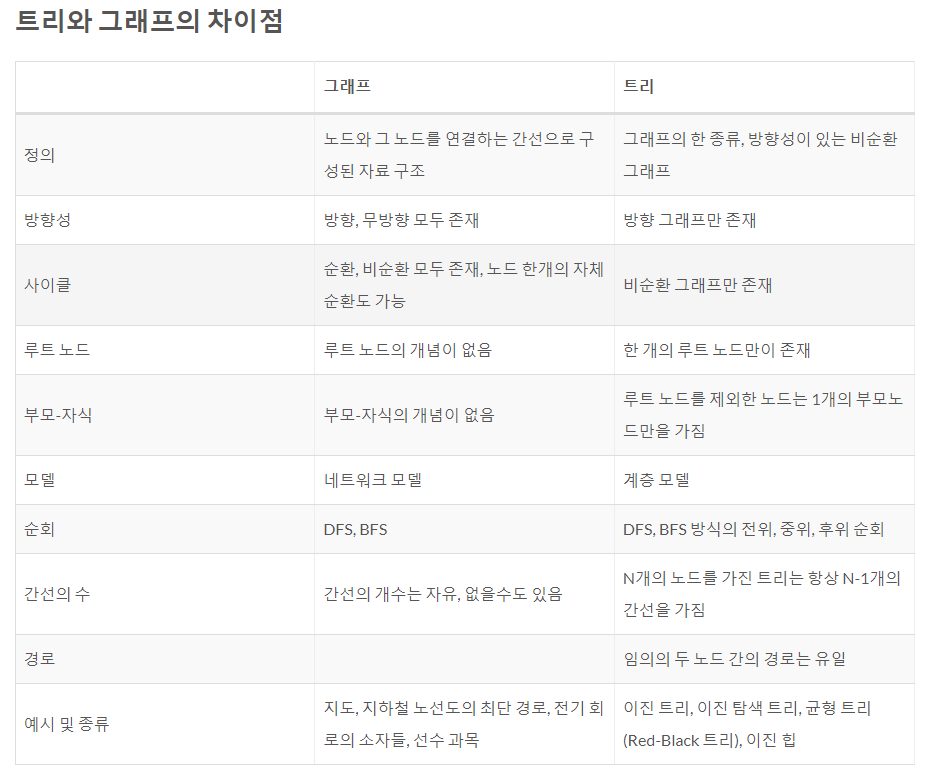
[python code review] 8주차(여행가자, 문제집, 최소 스패닝 트리)

https://www.acmicpc.net/problem/1976

1976번: 여행 가자

[union-find 알고리즘을 이용한 풀이]

def union(Parent, a, b):
    a = find(Parent, a)
    b = find(Parent, b)

    if a < b:
        Parent[b] = a
    else:
        Parent[a] = b

def find(Parent, x):
    if Parent[x] != x:
        return find(Parent, Parent[x])
    return x


n = int(input())
m = int(input())
parent = [i for i in range(n+1)]
for n1 in range(1, n+1):
    lst = list(map(int, input().split()))
    for j in range(n):
        n2 = j + 1
        # 0과 1 중에서 1인 경우, 두 노드를 union
        if lst[j] == 1:
            union(parent, n1, n2)
route = list(map(int, input().split()))
result = set()

for i in route:
    result.add(find(parent, i))
if len(result) == 1:
    print('YES')
else:
    print('NO')

*주의할 점

for i in route:
    result.add(find(parent, i)) 를 이용해 부모 노드가 누군지 찾는 과정에서 처음에 

for i in route:
    result.add(parent[x])와 같이 접근하여 틀렸다. 이처럼 접근하면 안되는 이유는 아래와 같은 반례 때문이다.

5
3
0 0 0 1 0
0 0 1 0 0
0 1 0 1 0
1 0 1 0 0
0 0 0 0 0
1 2 3

이 자료를 시각화하면 아래처럼 그래프가 생겼는데 

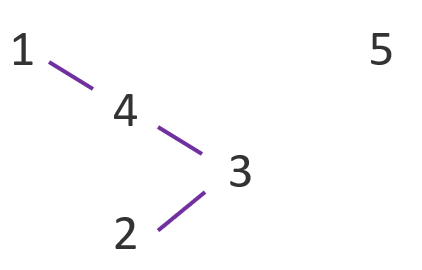
parent 리스트를 확인해보면 다음과 같이 저장되어 있다.

3의 부모로 2가 저장되어 있는데, 2의 부모는 1이기에

결국엔 3의 부모도 find 연산으로 올라가다 보면 최종 부모가 1이 된다.

그렇기 때문에 각 노드 별로 부모를 찾고 싶으면 parent 테이블에 담긴 정보를 확인하는게 아니라 find 연산으로 최종 부모를 찾아주어야 한다.   

푸는데 도움을 준 반례 출처 ->  https://www.acmicpc.net/board/view/49043 

 

https://www.acmicpc.net/problem/1766

1766번: 문제집

[위상정렬을 이용한 풀이]

진입차수가 0인 노드(먼저 풀어야할 문제)들을 heap에 넣어준다. ( 크기가 작은 순서대로 저장됨)

heap에서 어떤 노드를 꺼내면

해당 노드의 짝꿍(꺼낸 노드를 먼저 풀어야 쉽게 풀리는 문제)도 진입차수가 0이 되어 heap에 저장된다.

 

이때 가능하면 쉬운 문제부터 풀어야 한다. 라는 조건을 만족시키기 위해 최소힙을 사용했다.

import heapq

v, e = map(int, input().split())
graph = [[] for _ in range(v+1)]
indegrees = [0 for _ in range(v+1)]


for _ in range(e):
    a, b = map(int, input().split())
    graph[a].append(b)
    indegrees[b] += 1

heap = []
# 진입차수가 0인 노드 저장 (먼저 풀어야 할 문제)
for i in range(1, v+1):
    if indegrees[i] == 0:
        heapq.heappush(heap, i)

result = []
while heap:
    now = heapq.heappop(heap)
    result.append(now)
    # now를 풀고나서 쉽게 풀리는 문제 i에 접근 
    for i in graph[now]:
        indegrees[i] -= 1
        if indegrees[i] == 0:
            heapq.heappush(heap, i)

print(*result)

우선 위상정렬이 뭔지 까먹어서 공부한 뒤에 문제를 풀어봤다.

위상정렬 참고 자료 : https://freedeveloper.tistory.com/390

[이것이 코딩 테스트다 with Python] 36강 위상 정렬

위상 정렬로 접근하기 위해서 그래프는 우선 아래와 같은 조건을 만족해야 한다. 

1. 그래프의 간선은 방향을 가진다.

2. 그래프 내부에 순환이 없다.

 

위상 정렬 프로세스

1. 진입 차수가 0인 정점을 큐에 삽입한다.
2. 큐에서 원소를 꺼내 해당 원소에 연결된 간선을 제거한다.
3. 간선을 제거한 후 진입 차수가 0이 된 정점을 큐에 삽입한다.
4. 위 과정을 반복한다.

 

https://www.acmicpc.net/problem/1197

1197번: 최소 스패닝 트리

[MST를 이용한 풀이]

v, e = map(int, input().split())
edges = []
p = [i for i in range(v+1)]
for _ in range(e):
    a, b, c = map(int, input().split())
    edges.append((c, a, b))
# 비용 오름차순 정렬
edges.sort()


def union(parent, x, y):
    x = find(parent, x)
    y = find(parent, y)
    if x < y:
        parent[y] = x
    else:
        parent[x] = y


def find(parent, x):
    if parent[x] != x:
        return find(parent, parent[x])
    return x


total = 0
for cost, a, b in edges:
    if find(p, a) != find(p, b):
        union(p, a, b)
        total += cost

print(total)

최소 신장 트리(MST) : 노드 n개와 간선 n-1개로 구성된 사이클이 없는 부분 그래프.

                                 이때 노드를 잇는 간선 비용은 최소 비용이어야 한다. 

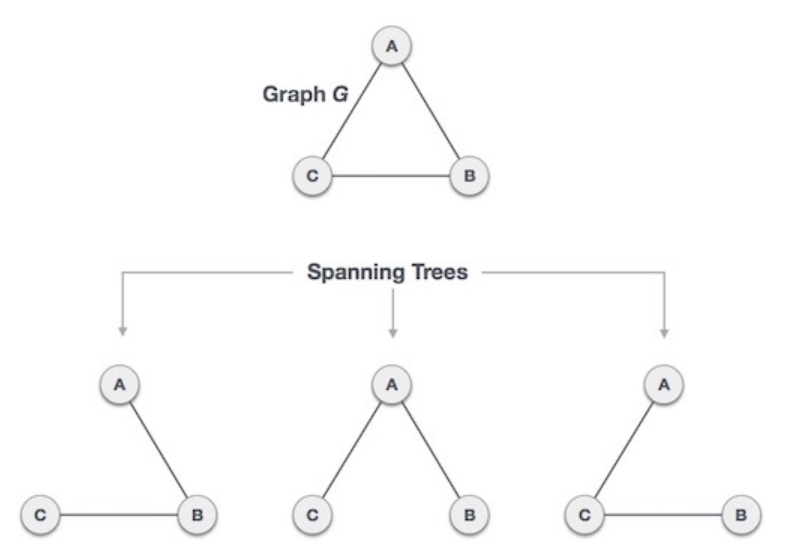
서로소 집합을 찾을 때 사용되는 union-find 알고리즘을 사용하면 된다. 

부모테이블을 자기 자신인 노드 값으로 초기화한 뒤 

연결된 노드 a, b에 대해 find 연산으로 찾은 부모가 다를 경우 union으로 하나의 집합으로 만들어준다.

이때 부모가 같은 노드끼리 연결해준다면 사이클이 발생하기 때문에 제외한다.  

MST 이해하기 쉬운 블로그 자료: https://techblog-history-younghunjo1.tistory.com/262

[Python] 최소 신장 트리를 찾는 크루스칼(Kruskal) 알고리즘