KEEP GOING
분류(Classification) vs 회귀(Regression) 문제 구분하기 (+평가 지표 정리 Confusion Matrix, Precision, Recall, f1-score, ROC, AUC, MAE, MSE, RMSE, ...) 본문
분류(Classification) vs 회귀(Regression) 문제 구분하기 (+평가 지표 정리 Confusion Matrix, Precision, Recall, f1-score, ROC, AUC, MAE, MSE, RMSE, ...)
jmHan 2023. 11. 16. 02:52분류
어떤 대상을 정해진 범주에 구분하여 넣는 작업
ex. 사람의 질병 유무 판별(1/0), 책의 IT 도서 유무 판별(1,0) 등
타깃값은 범주형 데이터여야한다.
타깃값의 데이터 범주가 2개라면 => 이진 분류
타깃값의 데이터 범주가 3개라면 => 다중 분류
분류 평가지표
1. 오차(=혼동) 행렬 Confusion Matrix
실제 타깃값과 예측한 타깃값이 어떻게 매칭되는지 확인
| 실제\예측 | 0 | 1 |
| 0 | 1291 | 74 |
| 1 | 151 | 110 |
실제로 매칭 안됐는데, 매칭이 안됐다고 예측한 경우: 1291건 (참 양성)
실제로 매칭이 됐는데, 실제로 매칭이 됐다고 예측한 경우: 110건(참 음성)
실제로 예측이 안됐는데, 매칭이 됐다고 예측한 경우: 74건 (제 1종 오류)
실제로 예측이 됐는데, 매칭이 안됐다고 예측한 경우: 151건 (제 2종 오류)
2. 정밀도 Precision
1로 예측한 경우, 얼마나 실제로 1인지를 나타낸다.
양성을 양성으로 판단 / (양성을 양성으로 판단 + 제 1종 오류)
정밀도 = 실제 true / 예측 true = TP / (TP + FP)
제 1종 오류가 중요하면 정밀도에 주목함
* 실제 False를 True로 판단/예측하면 안되는 경우에 중요한 지표로 활용 ( False가 중요한 경우)
ex. 스팸 메일 분류 - 스팸 메일(True)을 정상 메일로 봐도 되지만 정상 메일(False)을 스팸 메일로 알고 필터링하면 안 됨
* 쉽게 외우는 법 - 정예실
3. 재현율 Recall
실제 1 중에 얼마만큼을 1로 예측했는지를 나타낸다.
양성을 양성으로 판단 / (양성을 양성으로 판단 + 제 2종 오류)
재현율 = 예측 true / 실제 true = TP / (TP + FN)
제 2종 오류가 중요하면 재현율에 주목함
* 실제 True를 False로 잘못 판단하면 큰일나는 경우 중요한 지표로 활용 (True가 중요한 경우)
ex. 암 진단 - 암에 걸린 환자를 음성으로 판단하면 위험함. 대신 음성인 사람을 양성으로 판단해도 생명에 위험은 없음
* 쉽게 외우는 법 - 재실예
4. f1-score
정밀도와 재현율의 조화평균
2*(정밀도+재현율) / (정밀도+재현율)
1종 오류와 2종 오류에서 중요한 오류가 없다면 f1-score 활용
* 정밀도와 재현율이 한쪽으로 치우치지는 않았는지 검사
* 필요한 이유 - 정밀도와 재현율은 trade-off 관계. 한쪽 값이 커지면 다른 쪽 값이 작아짐.
5. ROC와 AUC
ROC: 참 양성 비율에 대한 거짓 양성 비율
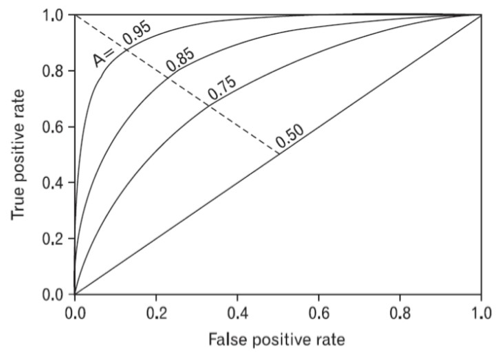
참 양성 비율(TPR) = TP(참 양성) / (TP(참 양성) + FN(거짓 음성))
실제 1인 것 중 얼마나 제대로 1로 예측했는지 검사
즉, 1에 가까울 수록 좋다
* FPR이 변할 때 TPR이 어떻게 변하는지를 나타내는 곡선
TPR은 민감도라고 부르고 재현율과 같은 의미이다.
TPR = TP / (TP + FN)
FPR = FP / (FP + TN)
임계값 (Threshold) 가 1이면 확률이 1일 때만 True 라고 예측하기 때문에
FP (실제 False인데 True라고 예측하는 경우) 가 0입니다.
결과적으로 FPR이 0이 됩니다.
임계값 (Threshold) 가 0이면 확률이 모두 True 라고 예측하기 때문에
TN (실제 False인데 False 라고 예측하는 경우) 가 0입니다.
결과적으로 FPR이 1이 됩니다.
따라서, 임계값을 1~0으로 거꾸로 조절하면서 그때마다 FPR에 따른 TPR을 계산후 곡선을 그립니다.
AUC = ROC 커브 아래의 면적
* 1에 가까울 수록 좋은 모형이라고 판단
회귀
독립변수와 종속변수 간의 관계를 모델링하는 방법
종속변수 즉, 타깃값이 범주형이 아니라 수치형이다.
독립 변수(설명변수, 예측변수)
영향을 미치는 변수
종속 변수(반응변수, 결과변수)
영향을 받는 변수
단순선형회귀
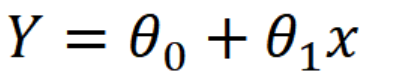
독립변수 하나와 종속변수 하나 사이의 관계를 나타낸 모델링 기법
다중선형회귀
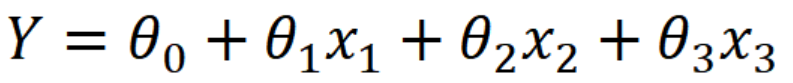
독립변수 여러개와 종속변수 사이의 관계를 나타낸 모델링 기법
회귀 문제에서는 주어진 독립변수(feature)와 종속변수(target) 사이의 관계를 기반으로 회귀 계수(세타)를 찾아야 한다.
회귀 평가 지표
1. 평균 절대 오차 MAE
실제 타깃값과 예측값 차의 절대값 평균
2. 평균 제곱 오차 MSE
실제값과 예측값 사이의 오차를 제곱한 값에 대한 평균
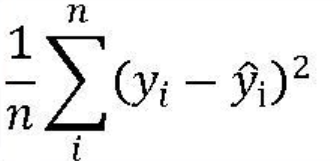
3. 평균 제곱근 오차 RMSE
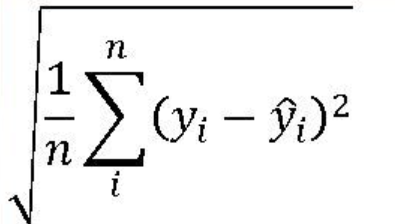
4. MSE에 로그를 취한 값, MSLE
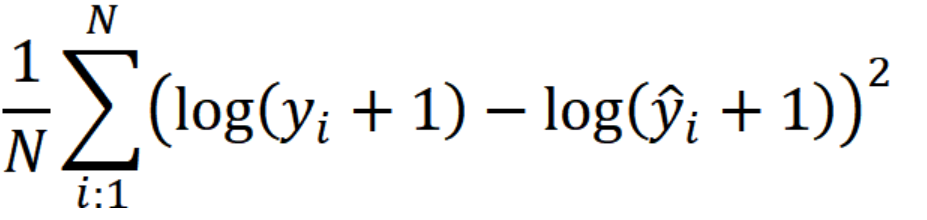
5. MSLE에 제곱근을 취한 값, RMSLE
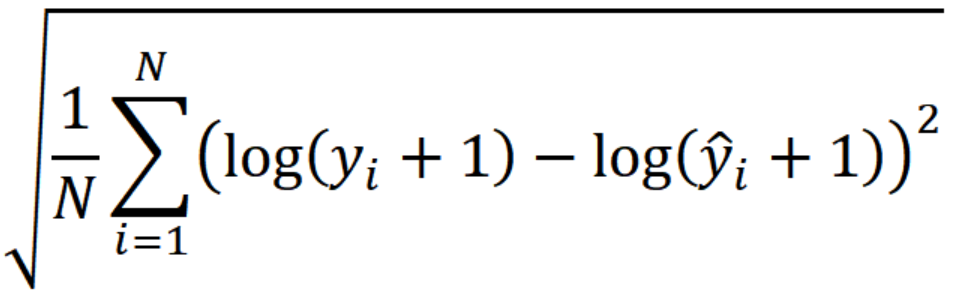
6. 결정계수 R^2
예측 타깃값의 분산 / 실제 타깃값의 분산
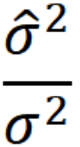
1에 가까울수록 모델 성능이 좋다
회귀 평가지표 코드
사이킷런의 metrics 라이브러리 활용
from sklearn.metrics import mean_absolute_error, mean_squared_error, mean_squared_log_error, r2_score
y_test = np.array([1,2,3,2,3,5,4,6,5,6,7,8,8]) # 실제값
y_pred = np.array([1,1,2,2,3,4,4,5,5,7,7,6,8]) # 예측값
MAE = mean_absolute_error(y_test , y_pred)
MSE = mean_squared_error(y_test , y_pred)
RMSE = np.sqrt(MSE)
MSLE = mean_squared_log_error(y_test , y_pred)
RMSLE = np.sqrt(mean_squared_log_error(y_test , y_pred))
R2 = r2_score(y_test, y_pred)
print(f'MAE :\t {MAE:.4f}')
print(f'MSE :\t {MSE:.4f}')
print(f'RMSE :\t {RMSE:.4f}')
print(f'MSLE :\t {MSLE:.4f}')
print(f'RMSLE :\t {RMSLE:.4f}')
참고:
[PYTHON - 머신러닝_캐글_분류와 회귀]★회귀 평가지표★분류 평가지표★ROC, AUC★RMSE (tistory.com)
'인공지능 > machine learning' 카테고리의 다른 글
| [ML] 부스트코스 Data Scientist Projects 2024 1주차 (0) | 2024.01.17 |
|---|---|
| [DL] 모두를 위한 딥러닝 노트 정리 (2/2) (0) | 2023.12.08 |
| [ml] 머신러닝 분류 classification 문제 뽀개기 (0) | 2023.11.15 |
| [ml] 머신러닝 예측 regression 문제 뽀개기 (0) | 2023.11.15 |
| [ml] 머신러닝 예측/분류 문제를 풀기 위한 Tips (0) | 2023.11.15 |






